Linear Regression in a different way

Trying to implement linear regression for a simple dataset without using existing regression library functions or the Gradient Decent Technique

Theory

Regression

A method of establishing relationship between 1 or more independant variables against one dependant variable

Linear Regression

Establishing a Linear relationship

Let’s try implementing the same:

Import the Google Drive to access your dataset

1
2
3

from google.colab import drive

drive.mount('/content/drive')

Drive already mounted at /content/drive; to attempt to forcibly remount, call drive.mount("/content/drive", force_remount=True).

1
2

import numpy as np
import pandas as pd

Reading the data

1

df = pd.read_csv('/content/drive/My Drive/slr_data.csv')

1

df.head()

.dataframe tbody tr th {
    vertical-align: top;
}

.dataframe thead th {
    text-align: right;
}


1

df.describe()

.dataframe tbody tr th {
    vertical-align: top;
}

.dataframe thead th {
    text-align: right;
}


1
2

import matplotlib.pyplot as plt
import seaborn as sns

1
2
3
4
5

plt.figure(figsize = (20,10))

sns.relplot(x = 'x', y = 'y', data = df)

plt.show()

<Figure size 1440x720 with 0 Axes>

png

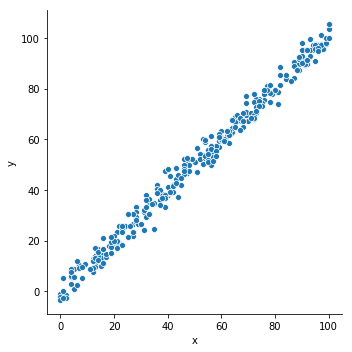
Linear Regression is all about finding a straight line that has the least Root Mean Square Value for the given data points => the line is to be existing between the extreme Y values to make sure the line is between the points in a given dataset

1

y_max = df.y.max()

1

y_min = df.y.min()

1

y_max

105.5918375

1

y_min

-3.4678837889999996

1

y_mid = (y_max + y_min) / 2

1

y_mid

51.0619768555

1

x2 = df.x.max()

1

x1 = df.x.min()

1

df.x.idxmax()

87

1

df.x.idxmin()

55

1

y2 = df.y[df.x.idxmax()]

1

y1 = df.y[df.x.idxmin()]

1

y2

105.5918375

1

y1

-1.040114209

1

slope_m = (y2 - y1) / (x2 - x1)

1

slope_m

1.06631951709

1
2

def lin_equ(x):
    return slope_m*(x - (df.x[df.y.idxmax()] + df.x[df.y.idxmin()]) / 2) + (df.y[df.y.idxmax()] + df.y[df.y.idxmin()]) / 2

1

df.head()

.dataframe tbody tr th {
    vertical-align: top;
}

.dataframe thead th {
    text-align: right;
}


1

lin_equ(77)

79.85260381693

1

lin_equ(21)

20.13871085989

1

lin_equ(22)

21.20503037698

1

lin_equ(20)

19.0723913428

1

lin_equ(36)

36.13350361624

1

df['y_pred'] = pd.Series(map(lin_equ, df.x.values))

1

df.head()

.dataframe tbody tr th {
    vertical-align: top;
}

.dataframe thead th {
    text-align: right;
}


1
2
3
4
5

plt.figure(figsize = (20,15))

sns.relplot(x = 'x', y = 'y_pred', data = df)

plt.show()

<Figure size 1440x1080 with 0 Axes>

png

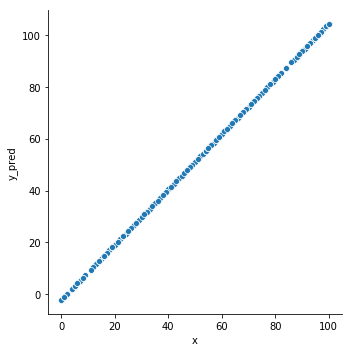
1
2
3
4
5
6
7

plt.figure(figsize = (20,15))

sns.relplot(x = 'x', y = 'y', data = df)

sns.lineplot(x = 'x', y = 'y_pred', data = df)

plt.show()

<Figure size 1440x1080 with 0 Axes>

png

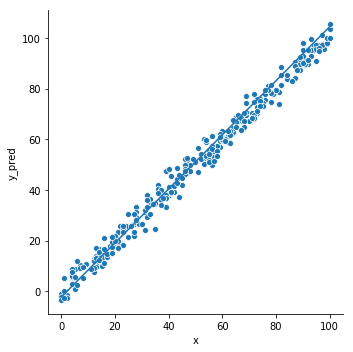
1

neg_err_sum = sum([i*i for i in df.y_pred-df.y if i < 0])

1

pos_err_sum = sum([i*i for i in df.y_pred-df.y if i >= 0])

1

neg_err_sum

1228.4737143905872

1

pos_err_sum

2396.9837025596657